R. Grothmann
Dieses Notebook beschäftigt sich mit verschiedenen geometrischen Aufgaben im Zusammenhang mit der Erdkugel. Es stellt sich heraus, dass aufgrund der Größe der Kugel im Verhältnis zu der Größe der betrachteten Änderungen manche Aufgaben nur sehr schwer zu lösen sind.
Zunächst wird eine Näherung für den Erdumfang und den Erdradius eingegeben.
>u=40008000; r=u/(2*pi);
Die erste Aufgabe besteht einfach darin, den Erdumfang um 1m zu verlängern. Um wieviel würde sich dann der Erdradius verlängern müssen?
Die Antwort ist unabhängig vom Radius, weil der Umfang linear vom Radius abhängt. Es sind ca 16 cm.
>1/(2*pi)
0.159154943092
Als nächstes Fagen wir, um wieviel der Radius zunehmen müsste, damit die Oberfläche um 1 Quadratmeter zunimmt. Hier erhalten wir schon den Fall einer sehr schlecht lösbaren Gleichung.
Aus der Formel für die Oberfläche
![]()
ergibt sich durch Ableiten die Änderung recht genau.
![]()
Es sind 9 Nanometer!
>longformat; 1/(8*pi*r)
6.24875024995e-009
Versuchen wir das Ergebnis ohne Ableitung exakt aus der Differenz der Oberflächen herzuleiten, so ergibt sich die Lösung einer quadratischen Gleichung. Leider berechnet der Computer die Lösung falsch, weil sich zwei Größen gegenseitig aufheben (Auslöschung).
>function O(r) &= 4*pi*r^2; >sol &= solve(O(r+x)-O(r)=1,x)
2
- sqrt(pi) sqrt(4 pi r + 1) - 2 pi r
[x = -------------------------------------,
2 pi
2
sqrt(pi) sqrt(4 pi r + 1) - 2 pi r
x = -----------------------------------]
2 pi
Wir werten nun beide Lösungen numerisch in Euler aus. Man erhält in der zweiten Lösung einen recht großen Fehler.
>sol()
[-12734941.9264, 5.92898365452e-009]
In Maxima ist das auch nicht besser, solange man gewöhnliche Gleitpunktarithmetik verwendet. Der Grund ist die Auslöschung bei der Subtraktion im Zähler.
>&rhs(sol[2]) with r=40008000/(2*%pi); &float(%)
5.9289836545249578E-9
Das wird erst besser, wenn wir in Maxima 32-stellig rechnen.
>&rhs(sol[2]) with r=40008000/(2*%pi); &bfloat(%)
6.2487502499500069466109384565857b-9
Allerding kann man mit einem einfachen Trick alles genau ausrechnen. Dazu erinnern wir uns, das das Produkt der Nullstellen den konstanten Koeffizienten ergibt, wenn der höchste Koeffizient 1 ist.
Damit erhält man dasselbe Ergebnis wie mit der Ableitung.
>1/(-4*pi*sol()[1])
6.24875024995e-009
Auch mit Hilfe des Intervall-Newton-Verfahrens erhält man eine sehr gute Einschließung der Nullstelle.
>mxminewton("2*r*x+x^2-1/(4*pi)",~0,1~)
~6.2487502499500036e-009,6.2487502499500102e-009~
Im nächsten Problem ziehen wir ein Seil, das um die Erde liegt und einen Meter länger als der Erdumfang ist, an einer Stelle hoch. Wie hoch kann man das Seil ziehen?
Mit ein wenig Geometrie erhält man eine Formel, die allerdings numerisch instabil ist.
![]()
>f &= sqrt(2*x*r+x^2)-acos(r/(r+x))*r
2 r
sqrt(x + 2 r x) - r acos(-----)
x + r
Das Bisektionsverfahren liefert aber dennoch eine Lösung.
>longformat; bisect(f,100,200,y=1/2)
121.438287177
Ebenso das Sekantenverfahren.
>longformat; secant(f,100,200,y=1/2)
121.438294686
Plottet man die Funktion in großer Nähe zu der Nullstelle, so sieht man, dass etwas faul ist. Es entstehen durch numerische Zufälligkeiten Artefakte.
>plot2d(f,a=121.4382,b=121.4383,adaptive=0):
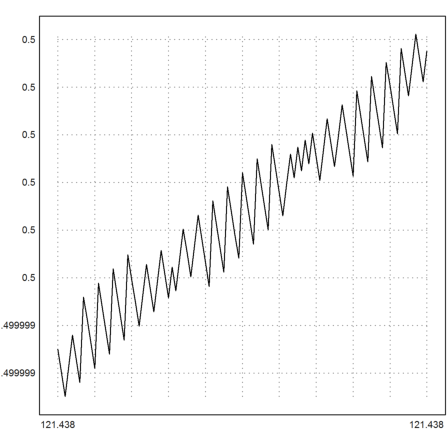
Folglich ist die Lösung maxima auf 5 Stellen nach dem Komma genau. Geht das besser?
Man kann das Problem auch über den Winkel lösen, den das Seil vom höchsten Punkt bis zu dem Punkt, an dem es aufliegt, bildet. Die Formel ist dann
![]()
Wir versuchen sie zu lösen.
>a=bisect("tan(x)-x-0.5/r",0,1)
0.00617598008012
Die zum Winkel gehörende Höhe berechnet sich ebenfalls nach einer einfachen Formel.
>(1/cos(a)-1)*r
121.438292701
Das Seil befindet sich ungefähr über eine Strecke von 79 km in der Luft.
>2*a*r
78650.7476591
Wieder kann man mit dem Intervall-Newton-Verfahren eine gute Einschließung erhalten.
>a=mxminewton("tan(x)-x-0.5/r",~0.006,0.007~)
~0.006175980080348,0.006175980080418~
Man kann damit die Höhe bis auf 7 Stellen hinter dem Komma einschließen.
>(1/cos(a)-1)*r
~121.438292707,121.438292717~
Als nächstes Versuchen wir die Oberfläche der Erde um 1 Quadratmeter zu erhöhen, indem wir einen Punkt nach außen ziehen.
Mit ein wenig Geometrie erhält man für den halben Winkel, der dabei nach außen gezogen wird die Gleichung
![]()
Allerdings wird die rechte Seite schlecht berechnet. Der kleine Summand wird von 2 "ausgelöscht".
>2+1/(pi*r^2)
2
Lösen wir das ganze zunächst in Maxima.
>sol &= solve(cos(a)+1/cos(a) = 2+ 1/(%pi*r^2),cos(a))
2 2
- sqrt(4 pi r + 1) + 2 pi r + 1
[cos(a) = ---------------------------------,
2
2 pi r
2 2
sqrt(4 pi r + 1) + 2 pi r + 1
cos(a) = -------------------------------]
2
2 pi r
Nun können wir den Winkel a in Euler problemlos berechnen. Die zugehörige Höhe, um die die Oberfläche nach oben gezogen werden kann, ist circa 56cm.
>acos(&rhs(sol[1])()), (1/cos(%)-1)*r
0.000420963107395 0.564189607781
Man kann aber auch einfach die linke Seite nach a entwickeln. Das ergibt.
>&taylor(cos(a)+1/cos(a),a,0,4)
4
a
-- + 2
4
Daraus ergibt sich
![]()
Also
>a=(4/(pi*r^2))^(1/4)
0.000420963113707
Die zugehörige Höhe ist bis auf 7 Stellen die gleiche.
>(1/cos(a)-1)*r
0.564189624748